
Than mathematicians, where the layperson is more likely to be familiar The word "fractal" often has different connotations for laypeople 6 Natural phenomena with fractal features.4 Common techniques for generating fractals.Fractal patterns with various degrees of self-similarity have been rendered or studied in images, structures and sounds and found in nature, technology, art, and law. Fractals are not limited to geometric patterns, but can also describe processes in time. Theoretical fractals are infinitely self-similar, iterated, and detailed mathematical constructs having fractal dimensions, of which many examples have been formulated and studied in great depth. There is some disagreement amongst authorities about how the concept Mandelbrot based it on the Latin frāctus meaning "broken" or "fractured", and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature. The term "fractal" was first used by mathematician Benoît Mandelbrot in 1975. The mathematical roots of the idea of fractals have been traced through a formal path of published works, starting in the 17th century with notions of recursion, then moving through increasingly rigorous mathematical treatment of the concept to the study of continuous but not differentiable functions in the 19th century, and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 21st century.
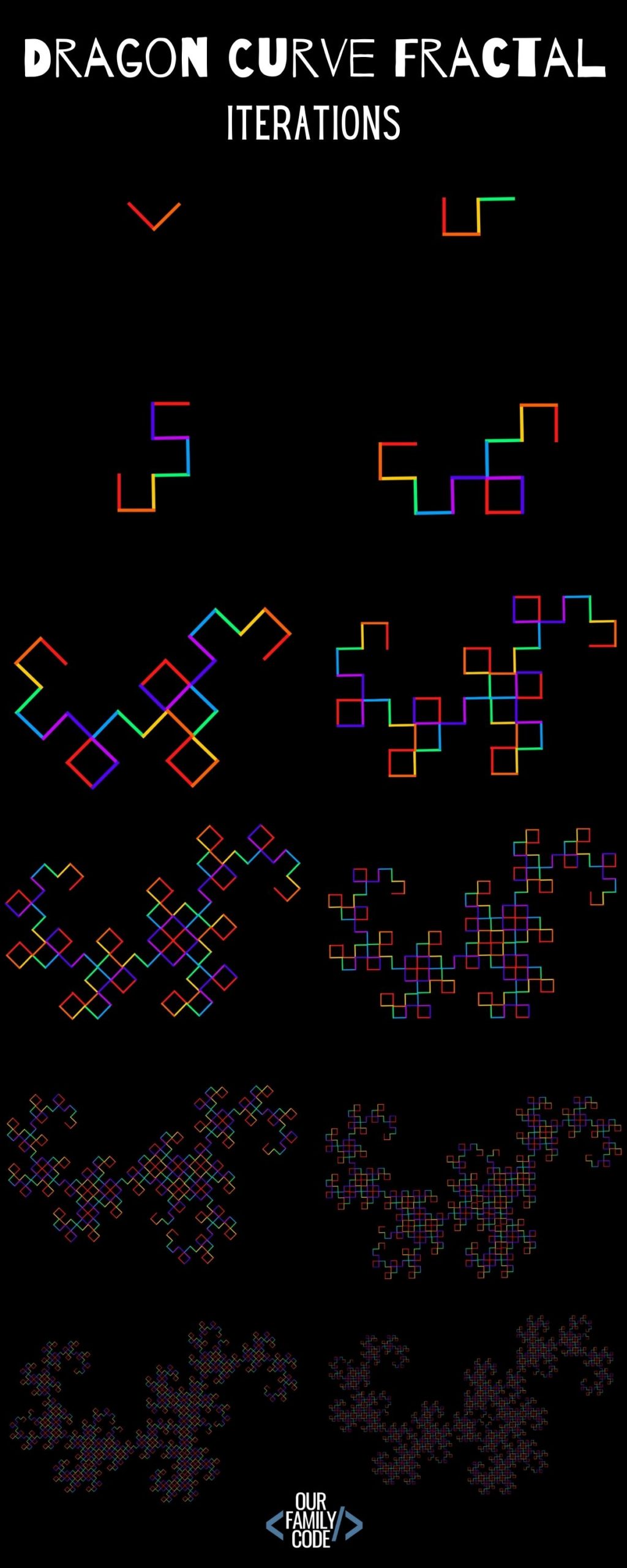
An infinite fractal curve can be perceived of as winding through space differently from an ordinary line, still being a 1-dimensional line yet having a fractal dimension indicating it also resembles a surface.

:166 18 Īs mathematical equations, fractals are usually nowhere differentiable, which means that they cannot be measured in traditional ways. The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Fractals may be exactly the same at every scale, or, as illustrated in Figure 1, they may be nearly the same at different scales. Fractals are typically self-similar patterns, where self-similar means they are "the same from near as from far".
#Dragon curve ultra fractal full
Even 2000 times magnification of the Mandelbrot set uncovers fine detail resembling the full set.Ī fractal is a mathematical set that has a fractal dimension that usually exceeds its topological dimension and may fall between the integers.


 0 kommentar(er)
0 kommentar(er)
